| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
- ObjectOptimisticLockingFailureException 처리
- RefreshToken
- interface
- multimodule testcontainers
- 알고리즘
- S3
- netty
- 낙관적 락 롤백
- 멀티모듈 테스트컨테이너
- spring aop
- aop
- jpa
- spring DI
- kotest testcontainers
- java
- DI
- redissonlock aop
- 백준
- Spring Cloud Gateway
- AccessToken
- @transactional
- springsecurity
- TestContainers
- ObjectOptimisticLockingFailureException
- 소수찾기 java
- 우아한 테크러닝
- OptimisticLock
- 형상관리
- Invalid property 'principal.username' of bean class
- 낙관적 락 재시도
- Today
- Total
조급하면 모래성이 될뿐
[프로그래머스] 멀쩡한 사각형 본문
문제 링크 : https://programmers.co.kr/learn/courses/30/lessons/62048
코딩테스트 연습 - 멀쩡한 사각형 | 프로그래머스
가로 길이가 Wcm, 세로 길이가 Hcm인 직사각형 종이가 있습니다. 종이에는 가로, 세로 방향과 평행하게 격자 형태로 선이 그어져 있으며, 모든 격자칸은 1cm x 1cm 크기입니다. 이 종이를 격자 선을 따라 1cm × 1cm의 정사각형으로 잘라 사용할 예정이었는데, 누군가가 이 종이를 대각선 꼭지점 2개를 잇는 방향으로 잘라 놓았습니다. 그러므로 현재 직사각형 종이는 크기가 같은 직각삼각형 2개로 나누어진 상태입니다. 새로운 종이를 구할 수 없는 상
programmers.co.kr
코드
package Programmers.Level2;
public class NormalSquare {
public static void main(String[] args) {
long answer = solution(1,3);
System.out.println(answer);
}//main
public static long solution(int w,int h) {
long wl = Long.parseLong(String.valueOf(w));
long hl = Long.parseLong(String.valueOf(h));
return (wl*hl) - ( wl+hl-gcd(wl,hl));
}
private static long gcd( long w , long h ) {
long small,big ;
big = w >= h ? w : h ;
small = w < h ? w : h ;
while ( small != 0 ) {
long nmg = big % small ;
big = small;
small = nmg;
}
return big;
}
}//class
제출 결과

후기
어려웠다.. 한 시간 정도 고민하고 다른 사람의 풀이를 참조해서 풀었다.
[프로그래머스] 멀쩡한 사각형 in python
파이썬으로 프로그래머스 풀기 :: 멀쩡한 사각형 문제 설명 가로 길이가 Wcm, 세로 길이가 Hcm인 직사각형 종이가 있습니다. 종이에는 가로, 세로 방향과 평행하게 격자 형태로 선이 그어져 있으며, 모든 격자칸은..
leedakyeong.tistory.com
저 문제를 보고 어떻게 저런 풀이를 생각해낼 수 있을지 놀라울 따름이었다.
빠르게 비슷한 유형의 문제들에 익숙해지는 것이 우선일 것 같다..
당장은 정확하게 이해가 되지는 않지만 다음에 유사한 문제가 나왔을 때의 접근방식을 나름대로 고민해보았다.
먼저 문제의 예시를 보았을 때, 동일한 패턴이 반복된다는 점을 캐치할 수 있다.
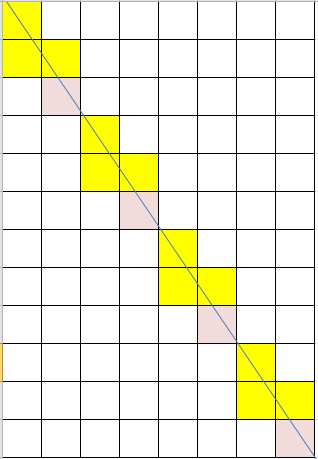
여기서 동일한 패턴이 반복되는 시작 좌표를 기록해보면 [0,0] 부터시작해서 [2,3] , [4,6] , [6,9] , [8,12]이 된다.
( 즉, 붉은색 네모의 우측하단 좌표이다.. )
- 먼저, 이 좌표에도 일정한 규칙이 있는지 고민해보았다.
- [0,0]을제외하고, 처음인[2,3]을 기준으로 x=2씩, y=3씩 증가되고있다.
- 2,3은 무슨 근거로 나온 걸까???
- 주어진 숫자 8(w),12(h)를가지고 2,3을 유추해보았다.
- 주어 진수 8,12를 4로 나누면 2,3이라는 숫자를 만들어 낼 수 있다..
- 그렇다면 주어진 가로,세로의 크기로 동일한 패턴이 반복되는 시작좌표를 구할 수 있는 규칙이 있다고 가정하고.. 그 규칙을 억지로 찾아보았다..
- 여기서 2,3이라는 숫자를 만들기위해 주어진 가로,세로를 공통적으로 4로 나누었다.
- 그럼 이 4는 무슨 기준인걸까..
- 일단 주어진 2개의 정수로 유추해 볼 수 있는 공통점은.. 최대공약수, 최소공배수 정도밖에는 없는것같다..
( 또 뭐가 있을까 ?? )
- 그렇게 찾아본 결과 4는 8과12의 최대공약수이다.
- 이거다! 라는 확신은 없지만.. 일단 주어진 조건으로 억지로 "최대공약수"라는 공통점을 찾아내었다.. 이제는 확신하기위한 검증을 더 해야겠다.
- 검증을 위해 w:7, h:14인 경우도 해보았다.
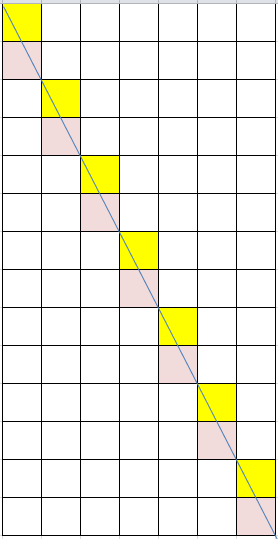
패턴의 종료지점이 되는 좌표
[1,2], [2,4], [3,6], [4,8], [5,10], [6,12] , [7,14]
- 시작점 1,2
- 7과 14의 최대공약수는 7
- W/최대공약수 , H/최대공약수를 하면 1,2가 맞다.
- 즉, 위의 정리가 맞다고 판단하였다.
- 정리하면, 문제에서 두가지 사실을 찾았다.
ㄴ 1. 대각선으로 잘랐을 때, 동일한 패턴을 가진 사각형이 영향을 받는다.
ㄴ 2. 최대공약수로 해당 패턴이 몇 번 반복되는지, 패턴의 구분점(좌표)을 구할 수 있다.
- 이제는 위의 두 가지 사실로 사용하지 못하는 블록의 개수만 정확하게 구해주면 된다....
- 그 방법은, 반복되는 패턴에서 잘리는 사각형의 규칙을 찾아야 한다는 것이다.
- 1번 예시를 보면 반복되는 패턴을 2,3을 하나의 사각형으로 그려본다면 2*3 크기의 사각형이 되고 이 사각형을 대각선을 잘랐을 때 사용할 수 없는 블록은 4개가 된다.

- 2번 예시는 1*2크기의 사각형에서 2개의블록이 영향을 받는다.

- 추가로 아래 5*2 사각형을 잘라보자.
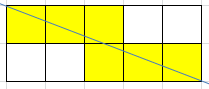
- 여기서 알 수 있는 사실은 N*M크기의 사각형을 대각선으로 잘랐을때 영향을 받는 블록은 [ N+M-1 ] 만큼의 블록이라는 것이다.
- 그 이유는 N*M크기의 블록을 대각선으로 자를때, 반드시 가로는 N만큼, 세로는 M만큼 가야하기 때문이다.
- ( 사각형을 대각선으로 자르면 왼쪽맨위끝~ 오른쪽 맨아래 끝으로가는데 그때 최대가로는 N, 최대세로는 M이니깐 !! )
- 그래서 대각선으로 자르면 가로N, 세로M만큼가서 N+M을하게되는데, 가로로 갈때랑 세로로 내려갈때 시작점은 똑같기때문에 중복이라서 -1을 해주는것이다 !!
- 어떻게 보면 당연한 사실이다. 아직까지도 그 규칙은 '진짜? 뭔가 허무한데..' 라는 의심이 들기도하지만 여러개의 사각형을 몇번 더 테스트해본결과 YES인것같다..
- 그렇다면 우리는 주어진 숫자로 영향을 받는 패턴의 사각형 범위 N,M을 구해서 한패턴에 몇개만 쓸수있다! 라는 사실을 구할 수 있다.
- 이제 이 패턴이 몇번반복되는지 알면되는데, 이것도 테스트를 해보면 우리가구한 최대공약수 만큼 반복하고있다.
- 이제 주어진 W*H로 최대공약수를구해서, 한 패턴당 몇개의 블록을 쓸 수 있는지 구해서 * 패턴이 반복되는 횟수(최대공약수)해주면 될것이다..
- 정리하면 [ ( W/최대공약수 ) + ( H/최대공약수 ) - 1 ] * 최대공약수 가 되겠다. = [ W+H-최대공약수 ]로 해도 결과가 같다.
- 최종 공식 : [ W+H-최대공약수 ]
- 이제 전체 사각형크기에서 위에서구한 값을 빼주면 정답이다.
- 링크의 블로그를 참조해서 이해를하였고.. 사실 아직도 명확하지는 않지만.. 같은 문제가 나왔을때 해결 할 수 있는 방법을 늘려갈 수 있으면 만족할 것 같다..
'Algorithm > Programmers' 카테고리의 다른 글
| [프로그래머스] 구명보트 (0) | 2019.12.11 |
|---|---|
| [프로그래머스] H-Index (2) | 2019.12.10 |
| [프로그래머스] 더 맵게 (0) | 2019.12.06 |
| [프로그래머스]소수 찾기 (0) | 2019.11.07 |
| [프로그래머스] 위장 (0) | 2019.11.07 |




